38 Third
As in A Fraction
Xiya Zhang
Formal Definition: Defining third in a fraction, as Rich, Barnett (2012) explained in Elementary mathematics, “A fraction represents parts of a whole. A third is one of three equal parts of something.” If you add three thirds together you get a whole.
Here is one-third written as a fraction:

In the fraction one-third, the top number, which is 1, is called the numerator. The bottom number, which is 3, is called the denominator.
Here is one-third circle:
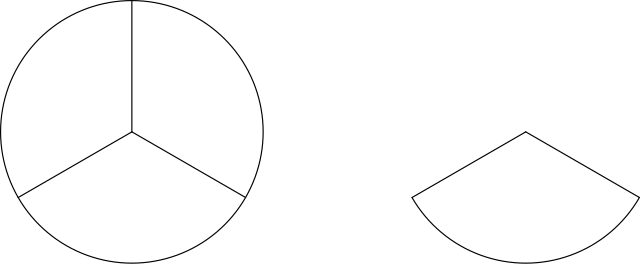
Kid-speak: We know that most kids have had to share at some point in their lives. They know how much half a cookie is. They know that when you share something with one other person, the 2 pieces should be the same size (equal). Getting that they understand this basic concept, we can build on it.
If “half” is 2 parts that are the same size, then “thirds” is 3 parts that are the same size. For example, if you have a cookie and want to share it with two friends, you would break it into 3 equal parts. This forms the basic construct for fractions. The top number in the fraction, the numerator, tells us how many parts we have. The bottom number, the denominator, tells us how many equal parts the whole is divided into. So, in the fraction one-third, we have 1 part out of a total of 3 equal parts. Understanding this concept helps us understand fractions better.

Cool Fact: It’s important to note that if we take a cookie and just draw three vertical lines to divide it, the three parts won’t be equal. True thirds mean the pieces must be the same size, but they might not be the same shape.

Way to learn about third:
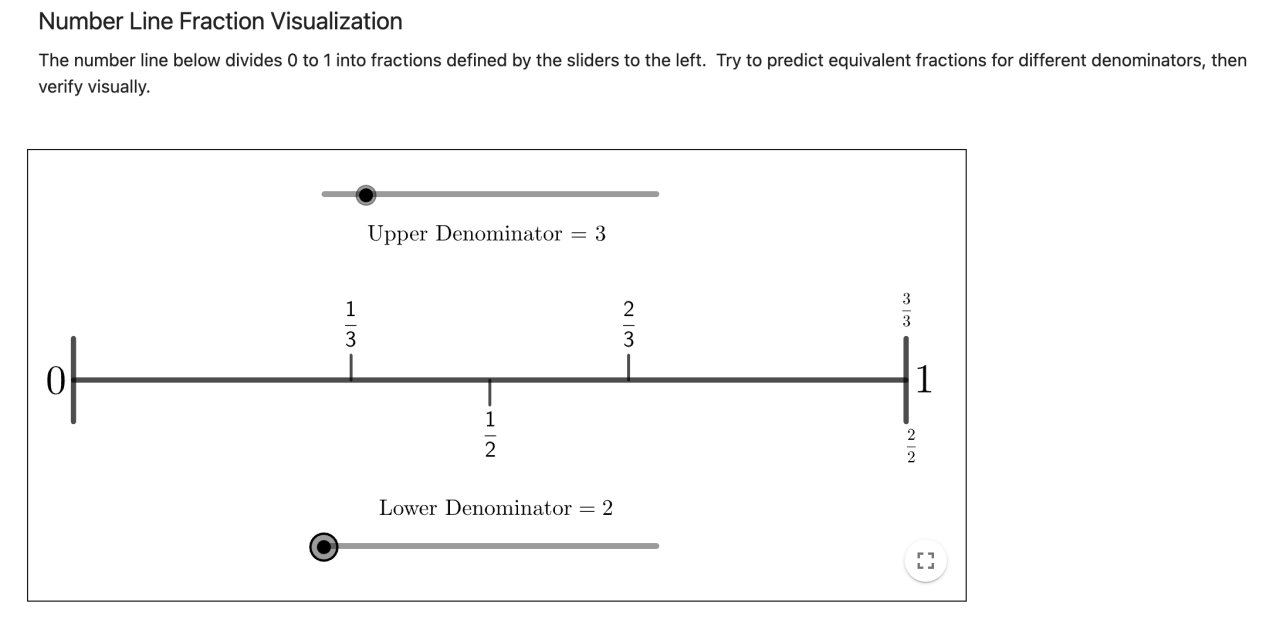
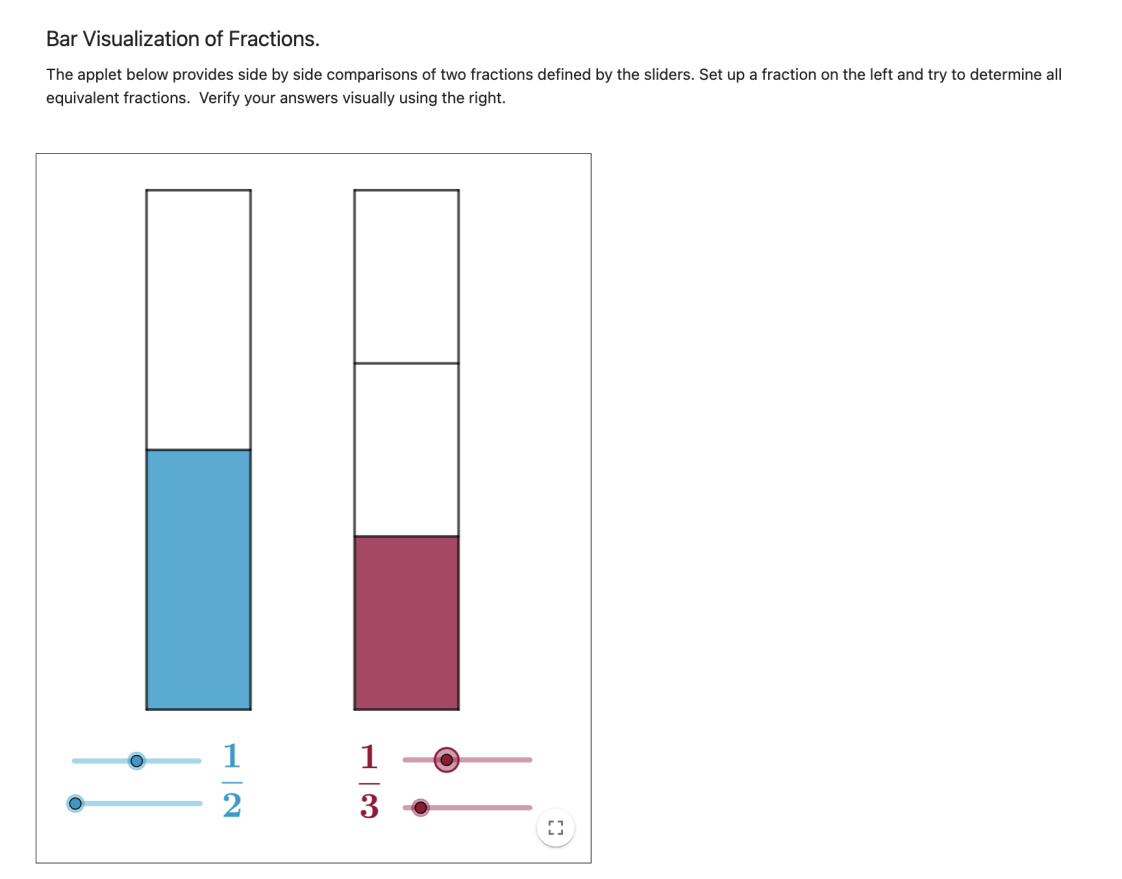
You can explore third and other fractions with the Fraction Exploration activities by Albert Navetta on Geogebra. The interactive applets “Number Line Fraction Visualization” and “Bar Visualization of Fractions” can help students intuitively understand the concept of 3 equal parts and what a third means. Using the Number Line Fraction Visualization, students can see how a unit length is divided into 3 equal parts, which helps them grasp the concept of a “third.” Similarly, the Bar Visualization of Fractions shows how a bar is divided into 3 equal parts.
These tools not only help students understand thirds but also allow them to compare one-third with other fractions, such as one-half, to understand the relative sizes of different fractions. Additionally, by changing the numerator and denominator, students can explore more complex fractions and see how these changes affect the size and representation of the fractions.
References:
Rich, B., Rich, B., & Schmidt, P. A. (2012). Elementary mathematics (Second edition / revised by Philip A. Schmidt.). McGraw-Hill.
BBC. BITESIZE. Finding a third. Retrieved from https://www.bbc.co.uk/bitesize/articles/zfc7dp3#zffqh4j
Albert Navetta. (2020, Jan 28). Fraction Exploration. Retrieved from https://www.geogebra.org/m/r79cn3zm
Attributions:
Figure2. “One third circle” by Apamodp is licensed under Creative Commons Attribution-Share Alike 3.0 Unported license
Figure 5. “Number Line Fraction Visualization” by Albert Navetta is licensed under a CC BY-NC-SA license
Figure 6 “Bar Visualization of Fractions” by Albert Navetta is licensed under a CC BY-NC-SA license

