Naive bayes

Dr. Nouhad Rizk

25 Naive bayes

The Naive Bayes algorithm comes from a generative model. There is an important distinction between generative and discriminative models.

Bayes Classifier

A probabilistic framework for solving classification problems
A, C random variables
Joint probability: Pr(A=a,C=c)
Conditional probability: Pr(C=c | A=a)
Relationship between joint and conditional probability distributions

Bayes Theorem

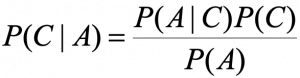
Naive Bayes Theorem Use Cases

Naive Bayes is great for very high dimensional problems because it makes a very strong assumption. Very high dimensional problems suffer from the curse of dimensionality – it’s difficult to understand what’s going on in a high dimensional space without tons of data. Example: Constructing a spam filter.

Example:

Given:

A doctor knows that meningitis causes stiff neck 50% of the time

Prior probability of any patient having meningitis is 1/50,000

Prior probability of any patient having stiff neck is 1/20

If a patient has stiff neck, what’s the probability he/she has meningitis?

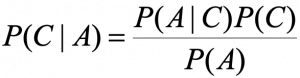
Example 2:

Given a new instance, predict its label

x’=(Outlook=Sunny, Temperature=Cool, Humidity=High, Wind=Strong)

P(Outlook=Sunny|Play=Yes) = 2/9

P(Temperature=Cool|Play=Yes) = 3/9

P(Huminity=High|Play=Yes) = 3/9

P(Wind=Strong|Play=Yes) = 3/9

P(Play=Yes) = 9/14

P(Outlook=Sunny|Play=No) = 3/5

P(Temperature=Cool|Play==No) = 1/5

P(Huminity=High|Play=No) = 4/5

P(Wind=Strong|Play=No) = 3/5

P(Play=No) = 5/14

Let’s start:

Given the fact P(Yes|x’) < P(No|x’), we label x’ to be “No”.

Problem: Players will play if weather is sunny. Is this statement is correct?

We can solve it using above discussed method of posterior probability.

P(Yes | Sunny) = P( Sunny | Yes) * P(Yes) / P (Sunny)

Here we have P (Sunny |Yes) = 3/9 = 0.33, P(Sunny) = 5/14 = 0.36, P( Yes)= 9/14 = 0.64

Now, P (Yes | Sunny) = 0.33 * 0.64 / 0.36 = 0.60, which has higher probability.

Naive Bayes uses a similar method to predict the probability of different class based on various attributes. This algorithm is mostly used in text classification and with problems having multiple classes.

How Naive Bayes algorithm works?

Step 1: Convert the data set into a frequency table

Step 2: Create Likelihood table by finding the probabilities like Overcast probability = 0.29 and probability of playing is 0.64.

Step 3: Now, use Naive Bayesian equation to calculate the posterior probability for each class. The class with the highest posterior probability is the outcome of prediction.

Python 3 Example: Please click here to see the Python3 Naive Bayes Example.