1 Particulate Organization of Matter. Essential properties of particles.

The world is a story of bound states.

What is a bound state? It seems best to give some examples first. A satellite orbiting its planet is a bound state formed as a result of gravitational attraction between the two objects. An atomic nucleus is an example of a bound state formed by nuclear forces, which are a combination of the so called “strong” and “electroweak” interactions, and quantum mechanical effects. Molecules and solids are particularly important for this Course. These are bound states formed as a result of an interplay of electromagnetic forces and quantum mechanical effects.

A common feature shared by those examples is this: A bound state is a union of at least two objects, such that the objects perform concerted, recurrent motions. In other words, these motions are synchronous and are oscillatory, cyclic. The Solar System, galaxies, molecules, solids, atomic nuclei are all examples of bound states. The union could last for just a few cycles or for many many cycles. In the former case, we call the union a weakly bound state, in the latter case a stable (or, more precisely, metastable) bound state. In either case, the breaking of the union, if any, will be a relatively rare event on the time scale of an individual oscillation.

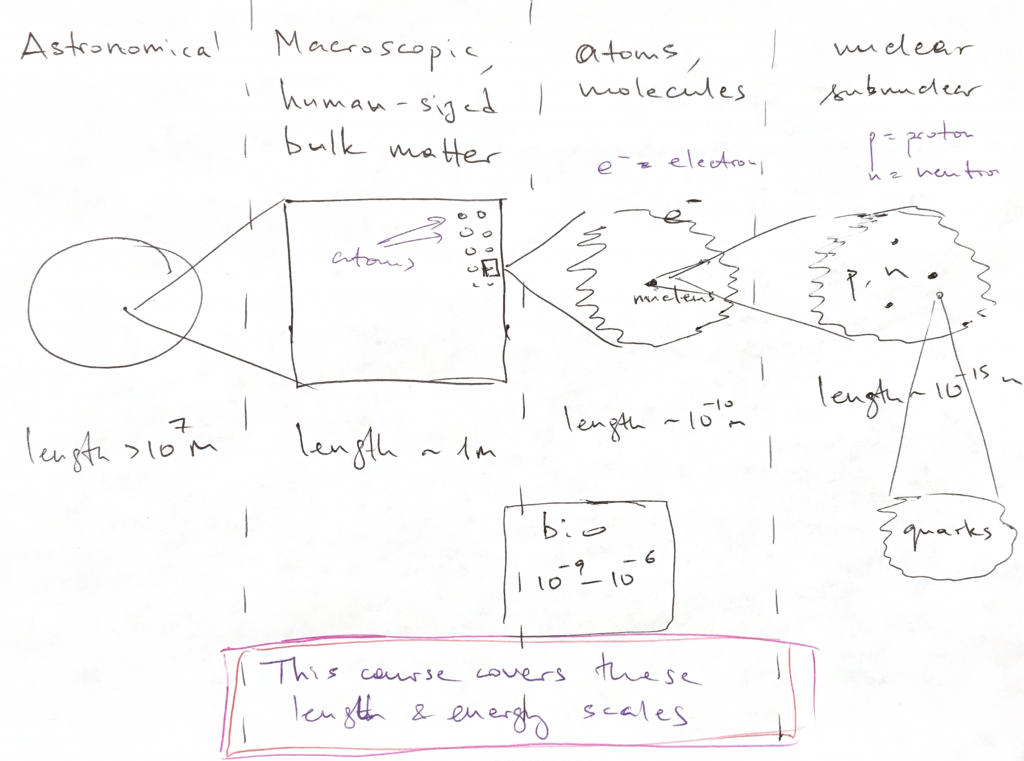
In a great variety of cases of interest, a bound state of two or more objects has a special property: It interacts with the rest of the Universe more weakly than each of constituent parts of the bound state would. For instance, two hydrogen atoms, when combined in a H molecule, are less likely to form a covalent bond with another molecule than a standalone hydrogen atom that has an unpaired electron to share. This may lead to an interesting situation. If it is indeed true that a bound state interacts only weakly with other entities, then the bound states corresponding to this new, weaker energy scale will generally be characterized by a different length scale as well. While the new energy scale is smaller, the new length scale is larger. This is a very simplified view of things yet it informally illustrates that physical phenomena form a hierarchy, both in terms of length scale and the associated energy scale. There are bound states at each level of the hierarchy: Here is an informal graphic illustrating this hierarchy of bound states, length-wise:

• • >10⁷ m: Planets, planetary systems, galaxies, the Universe. At these large scales, the gravity, the weakest force in the Universe, dominates. The effective charge is the mass itself. The other interactions, such as the electromagnetic interactions, are unimportant because the corresponding charges of macroscopic objects, such as planets, are zero.
  • 10^-10m to 10⁰ m:  Atoms/ solids/ liquids/ gases. Electromagnetic forces govern phenomena at these length scales. These length scales are the subject of this Course.
  • < 10^-15m: Nuclear and sub-nuclear phenomena, covered by Nuclear Physics and High Energy Physics. The dominant interactions here are the so called “electro-weak interactions” and the “strong interactions”

Two macroscopic objects ordinarily do not interact electrostatically because their electric charges are zero; they each consist of an equal measure of positively and negatively charged particles. There is a remnant of the electrostatic interaction that has to do with the fact that charges comprising an overall neutral system can move while remaining mutually bound; this motion is called “polarization”. The interaction caused by mutually-induced polarization of electrically neutral objects however decays rather quickly with distance. As a result, macroscopic objects interact largely through a much weaker, gravitational force and can be thought of as  particles that have only the gravitational charge, i.e., the mass. Similarly, a helium atom consists of two electrons, each charged at -1 (electron charge) and a nucleus charged at +2 (electron charges). In addition to being electrically neutral, a helium atom does not have an orbital that can readily accept an electron, nor is it too keen on giving up an electron, for reasons we will discuss later. As a result, a helium atom will not readily form a covalent and/or ionic bond. Instead, they will usually interact with the environment via a weaker force.

Thе physical situations described in the preceding paragraph are relatively clear-cut examples of bound states that act as  “particles”, i.e., objects whose internal interactions are significantly stronger than the interaction of the particle with the rest of the world. Conversely, the internal structure of a particle, if any, and at least some of the particle’s properties are only weakly perturbed by the environment. These properties, then, become convenient in discussing particles as standalone entities and, also, as starting points in discussing collections of particles. Informally speaking, the existence of properties that are not significantly perturbed by the environment of a particle means that the particle does not completely lose its “individuality” even when it interacts with the environment.

The notions of particles as long-lived bound states is decidedly modern and has resulted from research in Physics and Chemistry over the past two centuries or so. Yet well before the arrival of these modern ideas, people had already recognized that matter consists of bits that seem to be indivisible. The ancient Greeks (Democritus, Leucippus, ~500 BC) spoke of “atoms”, i.e., indivisible units of matter that remain in constant motion, while Lucretius, ~50 BC) discussed the gradual erosion of rocks. These early scholars thus noted that the mass and volume of macroscopic objects seems to change in discrete, even if tiny, units, but not continuously. Later work on electricity (Faraday, 19th century) proved that the electric charge also seems to change in discrete bits, namely, C (C=Coulomb). These three physical properties are, in fact, of prime interest for us in this Course. There is another property, called the spin, which is the intrinsic angular momentum possessed by small particles such as atoms and molecules, whose existence became apparent upon development of spectroscopy in the 20th century. Let us briefly review these four properties below:

What are some of these properties/descriptors (or “traits”, if you will) that individual particles could possess?

Mass:

A non-vanishing inertial mass reflects the property of inertia, i.e. the propensity to resist external attempts to change the state of motion of the object. For example, it takes a finite amount of work to force a stationary object to attain a finite velocity. Likewise, it takes an effort to stop a moving object. Gravitational mass: the effective charge for the gravitational interaction. Einstein showed that the inertial and gravitational mass are equivalent, which had been known before him but as a purely empirical notion as emphasized by Newton and Hooke, among others.

Volume:

The concept of volume is rather intuitive. Here we will often think of the volume as a quantitative measure of the amount of space occupied by a body or a collection of objects, such as a gas contained within a reservoir of volume . Another useful application is the excluded volume, i.e., the portion of space occupied by a particle and is not accessible to other particles. This is the origin of the so called steric forces (or, excluded volume interaction) in Chemistry.

Here we consider a useful example combining the concepts of particle, mass and volume, which deals with the specific volume and the related concept of the volumetric size.

The numbers of chemically distinct particles (atoms or molecules) that we generally deal with in a chemical or biological context are usually very very large, because those particles are very very small relative to a human. Thus it is often convenient to count those particles in large blocks. By convention, we count particles in blocks called moles, each mole containing particles. The latter number is often called Avogadro’s number:

The numerical value of was chosen specifically so that one mole of hydrogen atoms weighs 1 g.

Q:  How many H₂O molecules are contained in 1L of liquid water?

Thus, 1L = (10  cm) x (10 cm) x (10 cm) = 10^-3 m³ of liquid water weighs 1.00 kg = 1.00 x 10³ g.

1 mole of H weighs 1.00 g

1 mole of O weighs 16.0 g

1 mole of H₂O weighs 18.00 g.

Thus 1L of liquid water contains

Q:  What is the specific volume (volume per molecule) of liquid water?

By definition, the specific volume if found by dividing the total volume by the particle number :

Note the specific volume is the reciprocal of the concentration. Use this formula and the calculations above to check that the specific volume of liquid water is approximately 30ų.

Q:  What is the volumetric size of a molecule and what is the size of a molecule?

We can use the preceding exercise to evaluate how much “personal space”  a single water molecule has for itself, when surrounded by other molecules. For this, we must however assume a specific way the molecules are arranged. For concreteness, let us assume the molecule are confined to non-overlapping cells of cubic shape, all cells having the same size. By construction, the cells fill (or “tile”) the space,

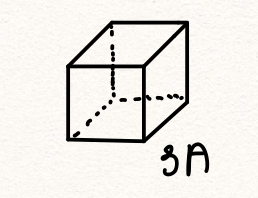
According to the calculation above, the volume of each of these cubic cells is 30ų

The lateral size of this cell, or the volumetric size of a water molecule in liquid water is, then (30 ų)^1/3 3Å.

If we further assume that water molecules are packed tightly (which is true, as we will see later), then the latter length also gives us an idea how large a water molecule actually is. For comparison, the O-H bond length is 1.0 Å, not bad!

It is necessary to emphasize that the specific volume, i.e., the volume per particle, is a useful measure of the molecular size only in condensed systems, namely, liquids and solids. In sufficiently dilute gases, the specific volume may exceed the molecular volume by an arbitrary amount. The volume of a gas is determined exclusively by the volume of the container!

Bonus Q: Given that the pH of water is 7 at normal conditions, that fraction of liquid water is dissociated at normal conditions?

According to calculations above,

[H₂O] = 55 M 55 mol/L

On the other hand, the pH of water is 7 at normal conditions, implying . This is much much less than the concentration of water molecules, implying only a tiny fraction of the latter are dissociated. Thus we obtain, to a good accuracy:

Electric Charge: Because most bodies are electrically neutral most of the time, we don’t deal with the static charge too often. Static electricity does reveal itself, nonetheless, if one rubs certain things against each other, such as the hair and the comb during brushing your hair. Most commonly, we encounter not the charge itself, but the current, which is the flux of charge. For instance, let’s estimate the amount of charge that runs through a typical household appliance in the course of time . By definition of the electric current, ,

where is the voltage and we used the fact that the power is evaluated as the product of the current and voltage. (I’ve eschewed some non-essential complications due to the current and voltage being alternating, not constant.)

Substituting 100 W for the power, 120 Volt, and sec, we obtain that 3×10³ C worth of electric charge will flow through a common appliance in hour. For comparison, the amount of charge that passes through a lightning bolt is only 10² C or so. Clearly, the lightning is so destructive not so much because of the overall amount of charge, but because of the huge currents that it induces. Conversely, the voltage generated between the comb and the hair during brushing is a couple of kilovolts yet it causes no damage because the currents involved are tiny. This is because the air, unless ionized, does not conduct electricity well. (Air does get ionized inside a lightning rod!)

Spin: The spin is yet another word for the angular momentum, which is the rotational analog of the momentum of translational motion. By definition, the momentum is the particle’s mass multiplied by its velocity :

Likewise, the angular momentum is defined as the moment of inertia times the angular velocity :

This formula is less confusing in the scalar form, which only involves the absolute values of the vectorial quantities: , where is now simply the rate of revolution times .

It turns out, empirically, that both momentum and orbital momentum are conserved (i.e. do not change) in the absence of interaction with the rest of the world. The conservation of angular momentum is vividly demonstrated by tucking in one’s arms while spinning on a rotating platform, which then results in an increase in the spinning rate:

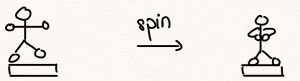
This can be quantified by noting the definition of the angular momentum for a compound object consisting of point-like objects:

where is the mass of object and is the distance of object from the axis of rotation. Clearly, as one tucks one’s arms in, the moment of inertia decreases. Since the product must remain constant, because of the conservation of angular momentum, the rotation rate must increase after the spinning person tucks in his/her arms.

It turns out that, like the electric charge, the orbital momentum changes in discrete bits as well, which is one of the most fundamental facts of Nature.

Now that we have introduced the concept of a particle, we are ready to state the main goal of the first part of this course, devoted to Thermodynamics. Here we will use basic notions of mechanics and statistics to connect phenomena taking place at the molecular scale with macroscopic thermal phenomena. In the second part of the course, Quantum Mechanics, we will ask about how those bound states we call atoms and molecules come about in the first place.